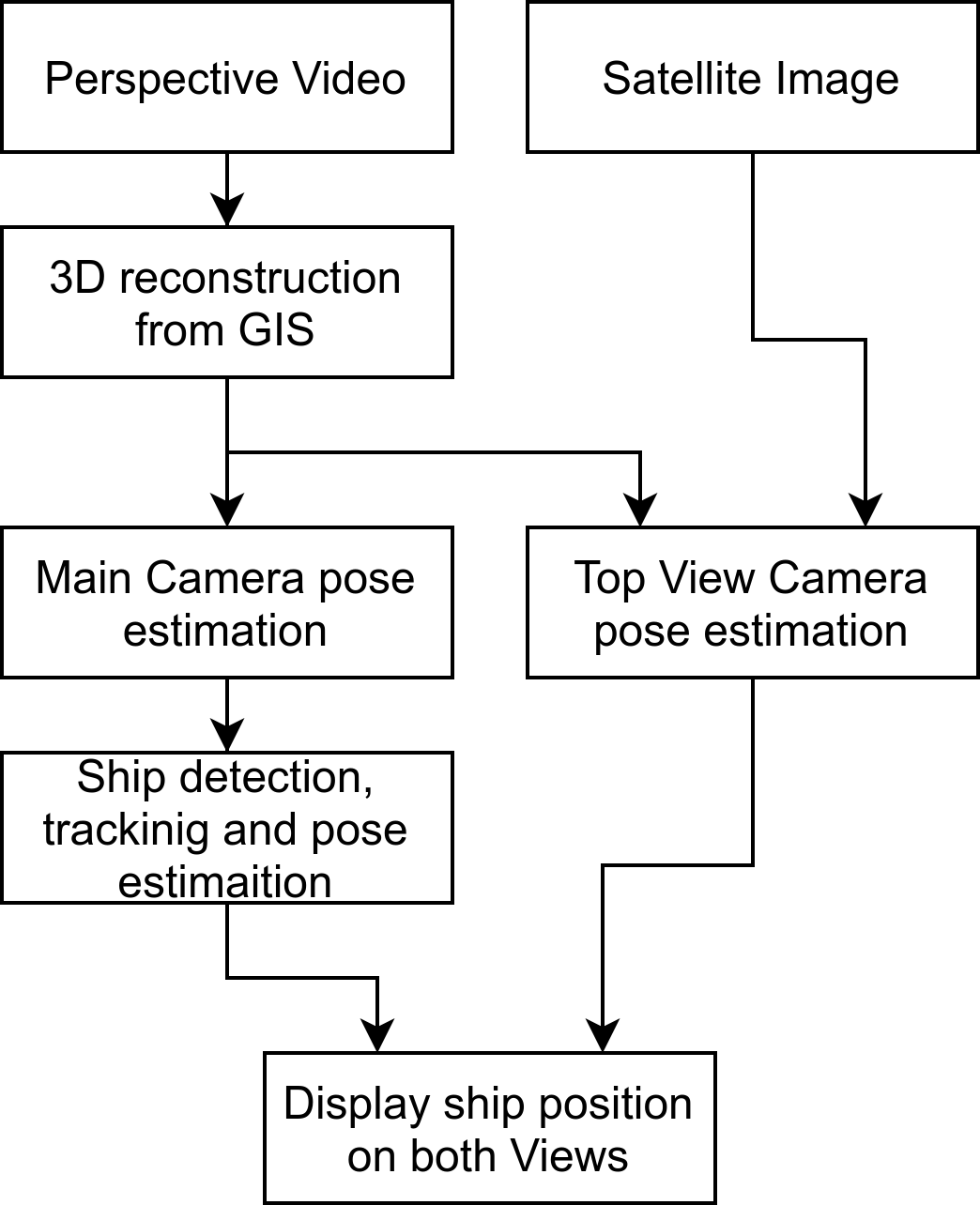
Recently we jump into a challenge to explore a specific application of computer vision: how can we estimate a top-view position of a ship from a given video from a fixed perspective camera? After some work we found our way, reaching what seems to be a quite reasonable result.
The following video is a simulation of our real-time processing running through a 60x speed video. On the left, we have the perspective view while on the right, the estimated top-view. The green rectangle is the tracked ship, the blue dot is the estimated position along its coordinates (relative to the perspective camera) in red:
The pipeline
To better explain whats going on here, we will breafily explain our pipeline for this solution:
First of all, we wouldn’t be calling it a challenge if the footage wasn’t nearly real footage. For sure the chosen footage needs to have great image quality, but its way more fun if there are no available information about the camera, the lenses, or its location, so all that needed to be estimated. For this application, we are using a small section from a Live video of the YouTube channel BroadwaveLiveCams.
But.. How can one estimate the camera pose with no prior information? It’s a bit tricky, but it is actually not that hard:
-
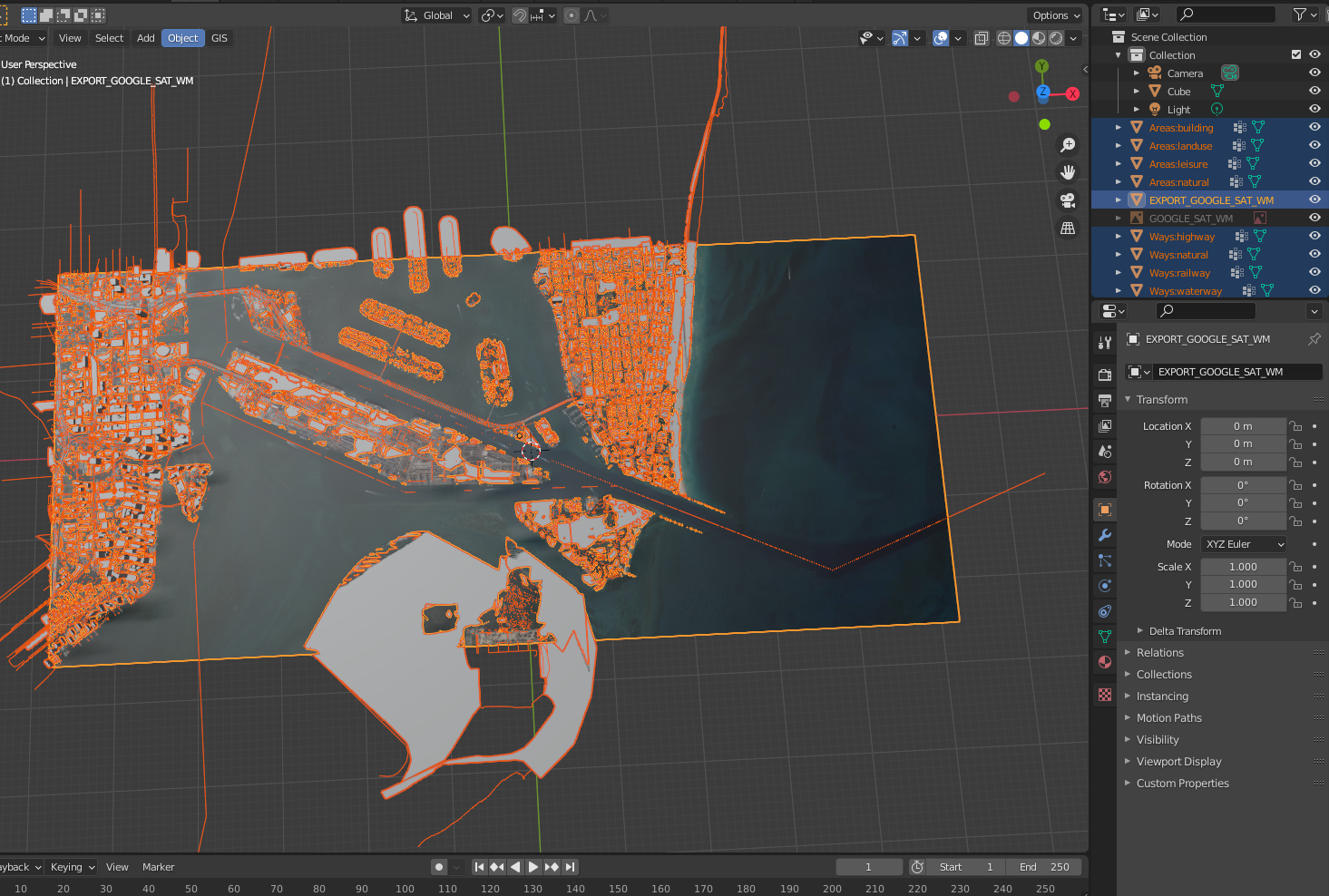
We first identified the site location and imported it to Blender using an open-source plugin called BlenderGIS, that gives us a near-enough 3D reconstruction for our location:
-
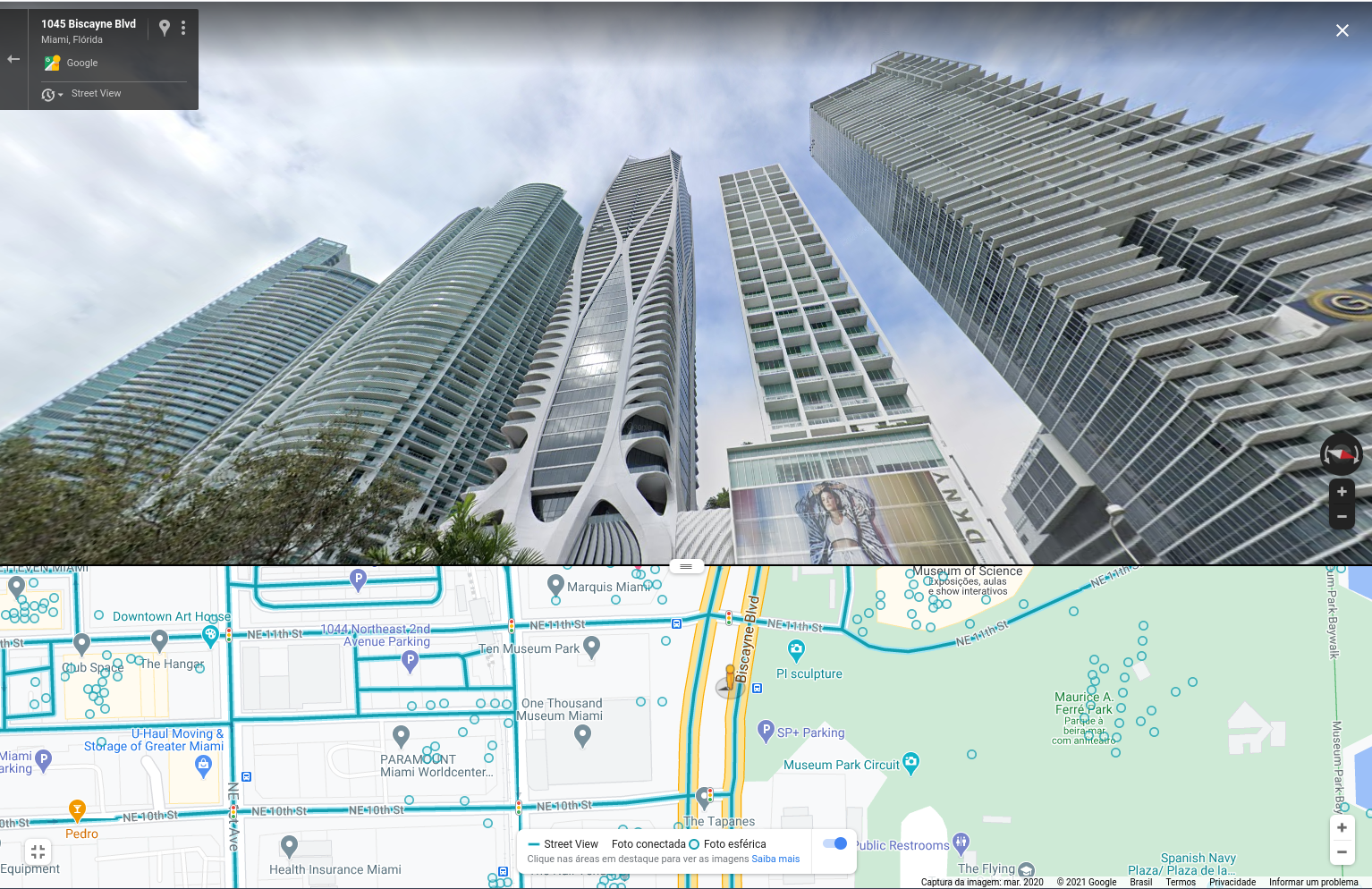
We took a walk around the site using Google Street View looking for a building that could give us a similar frame, and luckily in this case we had only one candidate:
-
Using the open source software called fSpy we manually matched the camera pose.
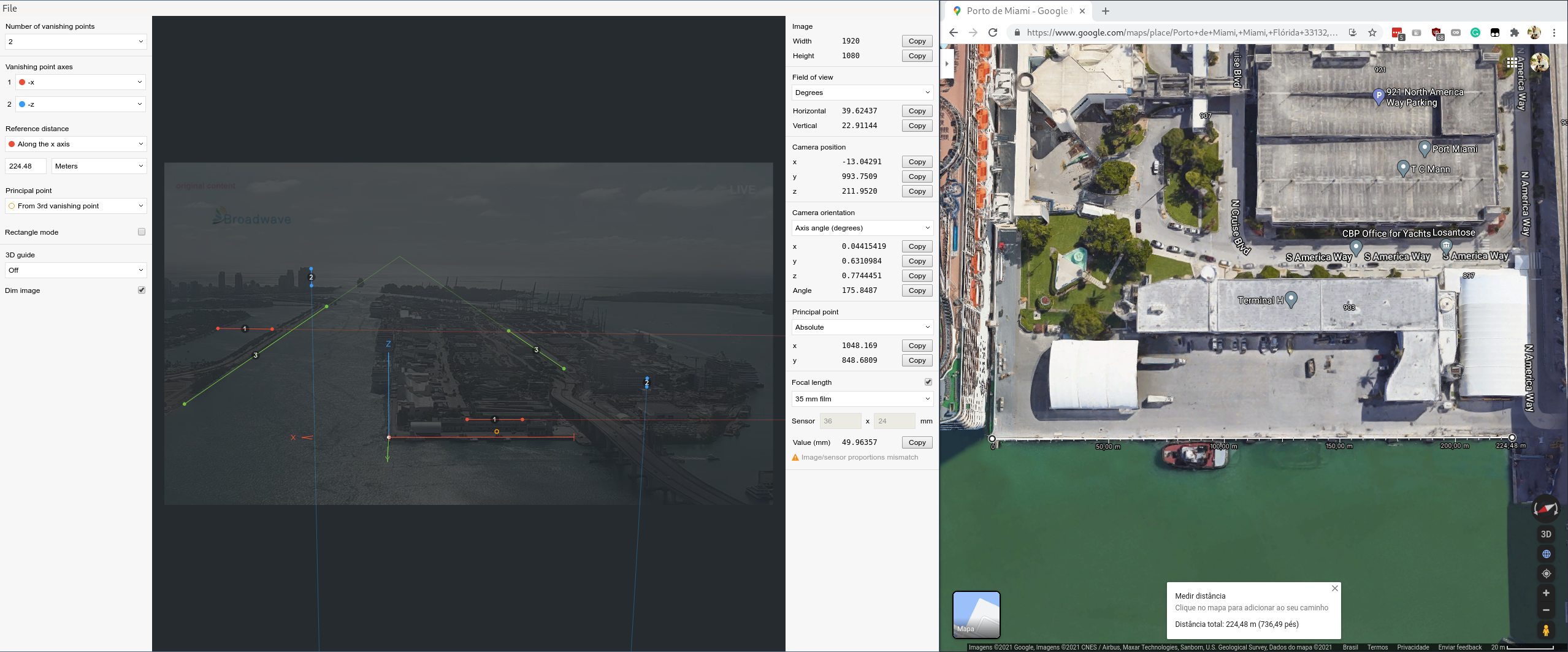
-
Then we imported to Blender (using fSpy-Blender add-on) and we confirmed our probable location:
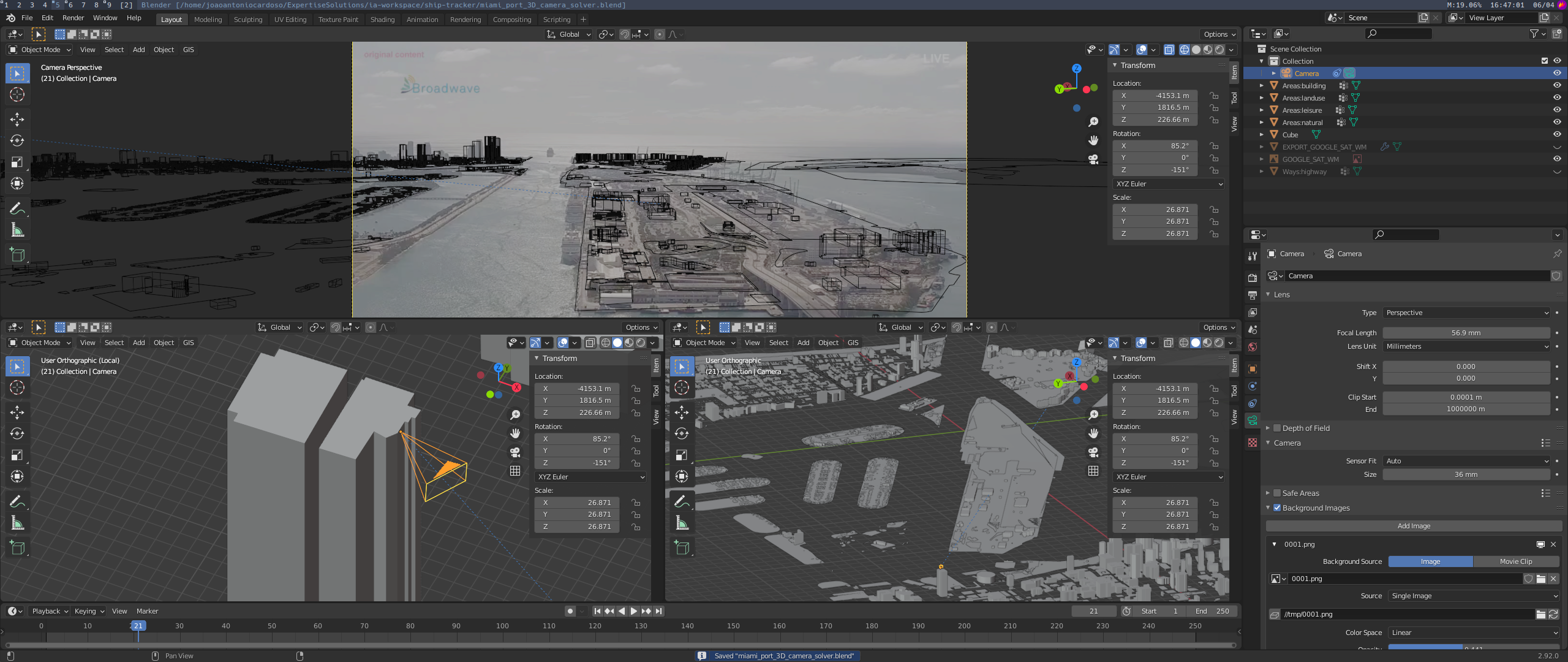
-
Further, we also explored another approach: getting the mached 2D and 3D positon of reference points (in red) on the reference image and used OpenCV’s routine
cv.solvePnP()to find the camera pose, then we reproject those 3D points to the camera, giving us the blue circles, that has its centers on the reprojected 2D point, and its radius represents its relative error: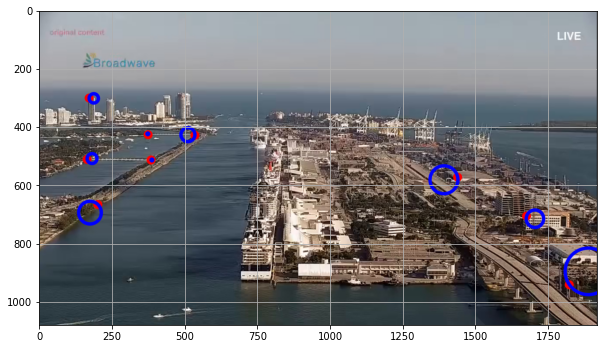
Then when we imported this estimation to Blender we got something coherent with our probable location, but this doesn’t seem to be as good as the other one: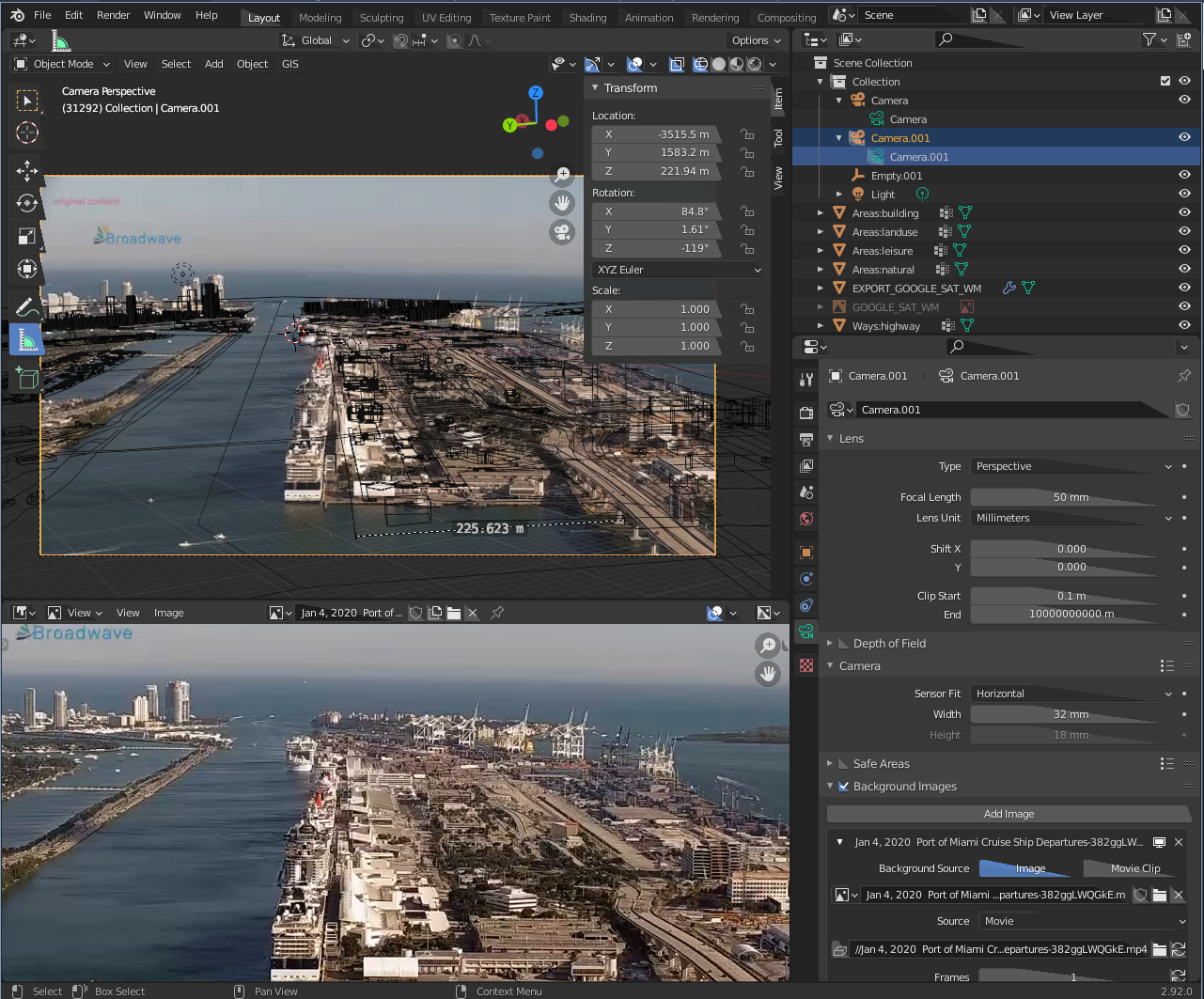
-
The satellite estimation is a bit easier given that it is so far away that it is almost an orthogonal view, so the exact altitude can be compensated with the lens size, means that we can find nearly infinite combinations that will nearly match our needs.
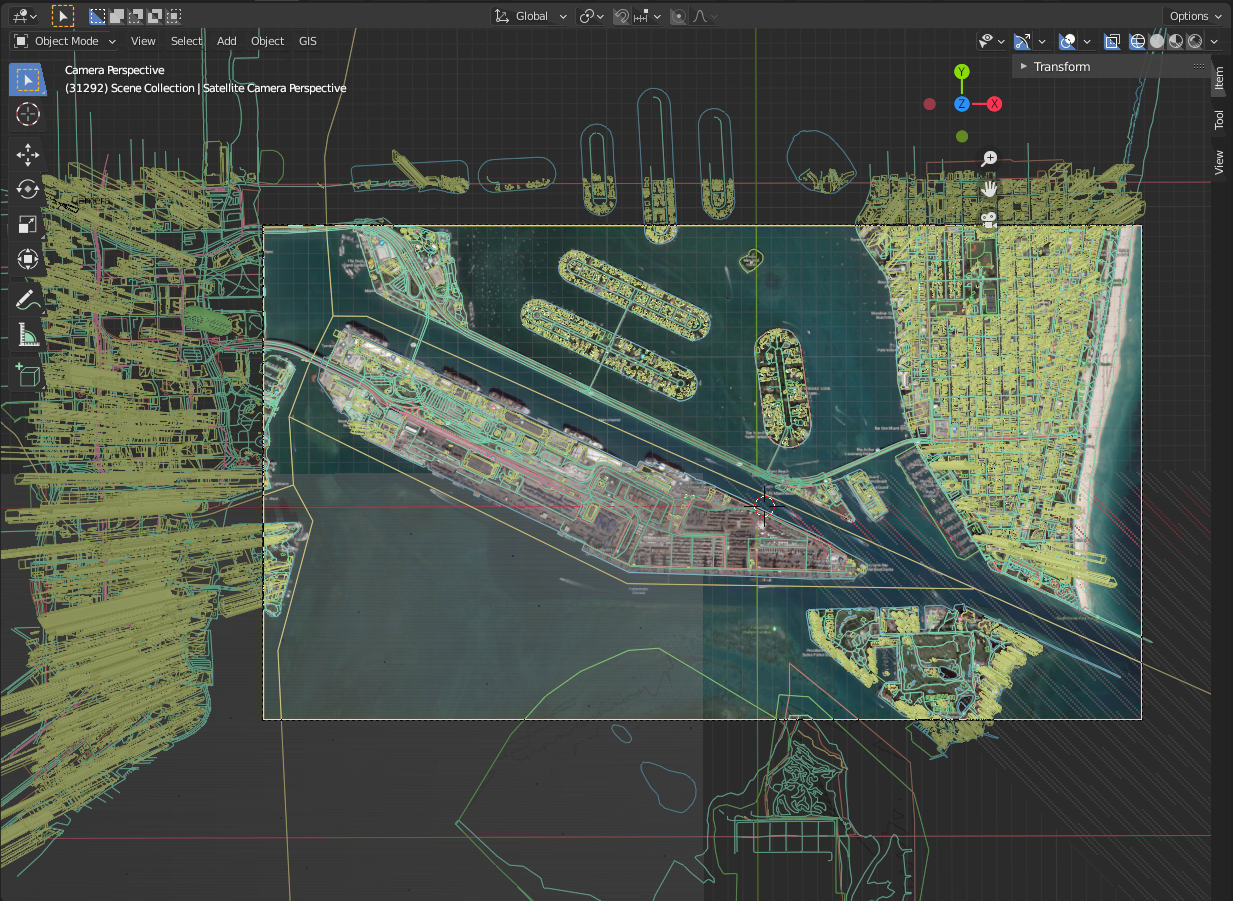
Ok, we have our scene on Blender, but we want to be able to process it with OpenCV!
OpenCV and Blender use different 3D orientation schemes, then you need to transform from one to another.
Blender has a very good Python API, so we wrote a script to deal with that and export our data to a text file.
On our Python scripts inside Blender we:
- automatically generate 1000 random cubes in the scene
- export to a file the 3D coordinates of the centroid of each cube
- project the centroid of each cube to both cameras
- export the pixel coordinates of each cube’s centroid for both cameras to a file
On our Python scripts outside Blender we:
- load the matched points
- using those 2D points we run
cv.findFundamentalMat()to get a mask to filter out the inlier points - using the filtered points we run
cv.findHomography()to get a homography matrix between the cameras - using the homography between the cameras we run
cv.perspectiveTransform()to transform the non-filtered main camera to the satellite view - compute the mean error between the original points and the projected ones.
The result can be seen in the following image. In red, the original points, in cyan, the reprojected points. The mean error was 0.54 px.

Fine, now we have the camera poses and a system that can project points from one to another, but…
How to estimate the ship coordinates?
With almost the same technique that we used to transform points from one perspective to another, we can find a homography matrix to project a pixel of a camera to the 3D water plane! See below:
- define four 3D points on the water plane
- project those points to the main camera using
cv.projectPoints() - using the projected points, find the homography matrix between the 3D points and the projected points
- now, we can use the homography to project a given pixel of the main camera to the water plane!
Conclusion
In this post, we saw how a specific problem in the computer vision field can be implemented, needing some analytical insights, and some manual steps along with the programming job of building an application.
As expected, real cases of computer vision are always challenging and sometimes require more than knowledge of the powerful OpenCV.